This post accompanies the paper “Spectrally approximating large graphs with smaller graphs” which appeared in ICML2018 (see talk here). For the latest results on graph coarsening (and demo/code) you may refer to this post.
In the graph world, data come in big sizes. This should be a cause for excitement: more data means more opportunities to derive insights and richer training sets for supervised learning algorithms.
In practice however, big graphs cause disdain to most. The reason is that the graph size -measured w.r.t. the number of nodes and edges
– determines the computational complexity of graph algorithms. Even the fastest algorithms struggle to deal with graphs consisting of tens or hundreds of thousands of nodes.
This computational challenge arises noticeably when it comes to applying machine learning on graph-structured data:
- Unsupervised learning tasks, such as clustering and non-linear dimensionality reduction, feature a super-linear complexity—typically between
and
.
Suppose for instance that we need to visualize a 100k node graph. If we try to embed the nodes in a 3D space using Laplacian eigenmaps then we will likely have to wait hours to inspect the result. This algorithm is thus an impractical choice for large-scale dimensionality reduction, irrespective of its ability to yield good embeddings.
- Supervised and semi-supervised learning tasks are usually solved with the help of localized aggregation primitives. These primitives are typically quite efficient and they can be used with any graph that fits a computer’s memory. Nevertheless, when the aggregation needs to be used repeatedly, the waiting times start to compound.
Graph convolution is a good example of this phenomenon. Training a graph convolutional neural network (GCN) involves using convolution again and again (every convolutional layer entails convolutions, where
are the number of input and output features respectively, whereas
is the batch size). For this reason, using GCN on large graphs can be a test of one’s patience.
The coarsening solution
So what can we do about it?
A common idea of approximation algorithms is that, instead of solving the original problem, solve a coarse problem of reduced size at a lower cost; then lift (and possibly refine) the solution.
For graphs this amounts to coarsening:
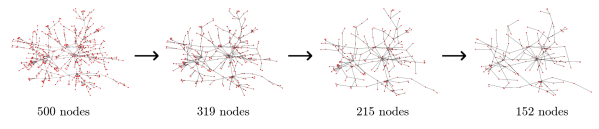
The above example shows how the number of nodes of a Barabasi-Albert graph (left) can be progressively reduced until a sufficiently small coarse graph
is obtained (right). Graph
will be a good substitute if it preserves the “global structure” of
and only lacks in “details”.
This approach has three benefits:
- Speed: Coarsening is usually very fast (
operations)
- Interpretability: Coarse variables have a meaning (in contrast to random projections).
- Simplicity: We can use the same algorithm to process
as
.
The mystery
It will be of little surprise that graph coarsening is well-known, both by the algorithmic and machine learning communities.
Whether the purpose is to partition and visualize billion-node graphs [Wang et al. 2014], to generate multi-scale representations of graph-structured data [Shuman et al. 2015], to solve large linear systems involving Laplacian matrices [Livne and Bandt 2012], or to do pooling in GCN [Defferrard et al. 2017, Simonovsky and Komodakis 2017], a large number of works use coarsening. (These references are of course only representative.)
Being so widely known, one would expect a concrete understanding of what information coarsening destroys and, moreover, how this loss affects learning algorithms.
Unfortunately, to-date no such theory exists.
The coarsening algorithms currently in-use are heuristics—they have been found out to work well experimentally, but there is neither any concrete understanding of how they affect learning algorithms nor any conclusive evidence that they cannot be improved.
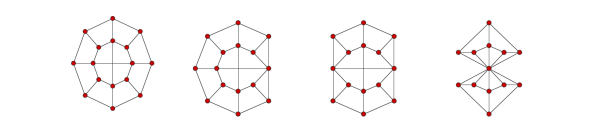
The example above shows how coarsening even few vertices may deform the graph structure. This is an issue for GCNs, that commonly aim to reduce the number of vertices by a factor of 2 at each layer. Here, the leftmost graph, consisting of 16 vertices, is progressively coarsened to 13 vertices using edge contractions.
A spectral perspective
In the paper “Spectrally approximating large graphs with smaller graphs” which appeared in ICML2018 (see talk here), we asked the following question:
How does coarsening affect the spectrum of a graph?
By spectrum, I mean the principal eigenvalues and eigenvectors of the graph Laplacian.
Why spectrum? There are a two primary reasons why I decided to approach graph coarsening using spectral graph theory:
- The spectrum plays a fundamental role in modern graph theory. Graph theorists love to quantify the global properties of graphs through the spectrum of a graph. For instance, the spectrum can be used to capture the community structure of a graph, the presence of hubs and bridges, and the susceptibility of a network to epidemics, among others.
- Numerous learning algorithms use it (c.f., clustering, embedding, multi-scale representation). A case in point, graph convolution carries along an elegant spectral interpretation (see this post). Knowing how far is the spectrum of
to that of
effectively means that we understand to what extend we may coarsen a graph without significantly affecting the learning algorithms that use it.
Understanding how changing a graph (in this case by coarsening) affects its spectrum is a difficult problem. The few results that are known concern the eigenvalues and are quite pessimistic [Chung 1997; Chen et al. 2004].
New insights
In a nutshell, we discovered that to guarantee spectrum approximation it is sufficient to check whether a simple property holds.
The restricted spectral similarity (RSS) property asserts that the Laplacian matrices of and
behave similarly (up to the RSS constants) with respect to an appropriate set of vectors.
Interestingly, the smaller the RSS constants are, the better the approximation!
This finding has intriguing consequences:
- Since the RSS property is relatively simple to verify, one can use it to derive approximation guarantees for current heuristics. In the aforementioned paper, we discuss how (a randomized variant of) the well-known heavy-edge matching heuristic finds meaning as a relaxation of the RSS constant minimization problem.
- For the particular case of spectral clustering, our results imply that coarse eigenvectors can be used to derive good quality assignments even without refinement—this phenomenon has been experimentally observed [Karypis and Kumar 1998], but until now lacked formal justification.
You can also find code reproducing the experiments of the paper here.
What’s next?
The RSS property opens up new ways, not only to understand coarsening, but also to optimize its operation.
In the follow up post “Graph coarsening with spectral and cut guarantees“, I will attempt to answer a question I have been thinking a lot about:
How should a graph be coarsened so that its spectrum and cuts are preserved?
There will be more pictures this time, I promise.


Thank you so much for such an easy explanation of graph coarsening which aided in my understanding of the intricate working of Graph convolution as well!!
I am happy that this was useful Anirudh!
Thhis was great to read